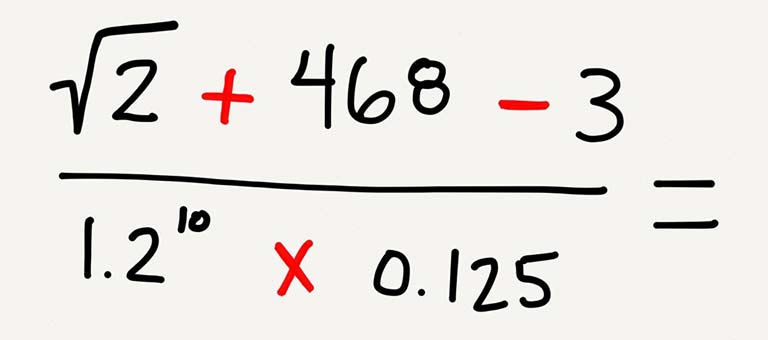
In mathematics, who decided the order of the operators? Who made the decision that a square root should jump the queue over addition? Who ruled that division would always trump addition and subtraction? Is it a mathematical necessity (for want of a better phrase) like 1+1=2? Or was there some ancient synod of mathematicians who came together to agree the pecking order of operators? Or was it like idioms in spoken language that come to have an agreed meaning after public acceptance through use?





The order of operations falls logically out of group theory. When you get past arithmetic and you start to think in terms of terms, it becomes obvious. A term is a functional unit of an equation. It’s components are held together “tightly” by multiplication. Terms are held together with other terms “loosely” with addition. A terms degree is the highest power of one of its variables.
Furthermore, multiplication is just addition looped, and raising powers is just multiplication looped. So there is a structure to these operators beyond simple arithmetic. It makes perfect logical sense that we perform the higher order operations (i.e. powers and multiplication) first.
Finally, addition and subtraction are the same thing. Multiplication and division are as well. So are powers with roots. You should read about group theory. It’s a part of abstract algebra. It’s really interesting. There is a group that has 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 elements and is a one-off in mathematics. It is an anomaly. There are exactly 26 of these one-offs and the monster is the largest. Now, I’m not saying that there are just 26 that we’ve found. They have proven that there are exactly 26, no more, no less.
@ Jordan,
Wholly logical explanation. To be honest, I was really hoping that Archimedes was drinking wine with Euclid and in his drunkenness, lost the toss of the coin on how operators should function.